Hi Mr Tom
I am going to review this entirely before posting with more coffee. I still don't have it right.
OK, with more coffee and a careful and a number or crosschecks I think I have the tolerance equations correct. They are not complex and simple to implement in software. It was close to what I had before yet not correct.
To be honest, this probably is not going to be of great interest to the majority of folks yet the answer to what was "tolerance" in Photoshop has been elusive and was just bugging me. For a given value of "Tolerance" and a sample point, "Just what RGB values will be picked up in the selection. The equations below and some following visualizations may help answer that question. I even included some 3D images of the RGB capture range.
First here are the equations (updated and corrected from prior post):
Using ∆ = Delta
Absolute Value = | number | (positive numbers left alone, negative numbers negated to a positive value)
T = Tolerance
<= means less than or equal
Rsample = the R value of the sampled point with e.g. magic wand
Gsample = the G value of the sampled point with e.g. magic wand
Bsample = the B value of the sampled point with e.g. magic wand
Rimage = the R value of Image Pixel
Gimage = the G value of Image Pixel
Bimage = the B value of Image Pixel
∆R = Rimage - Rsample
∆G = Gimage = Gsample
∆B = Bimage - Bsample
The above 3 ∆ values can be thought of as the RGB distance an Image Pixel is from the Sampled Point.
A pixel is within a selection with a given tolerance T, if all the following 6 conditions are met
| ∆R | <= T
| ∆G | <= T
| ∆B | <= T
| ∆R - ∆G | <= T
| ∆G - ∆B | <= T
| ∆R - ∆B | <= T
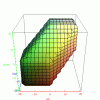
If all that was used were the first 3 equations, all this would be is a cube bounding box in RGB space around the sample point in RGB space with a distance from the center sample point to each edge of the cube. This would appear as the image below (example used a T value of 19 and the origin of 0,0,0 was set to the center sample point for ease of plotting):

However, the Tolerance function in Photoshop is more restrictive. When you include the last 3 boundary equations, the actual RGB values around a sample point that are included appear as the following image:

I have a couple animated GIFs below rotating this image looking from both above and also below the 3D image. The bounding shape ends up being two cubes with edge size of "Tolerance" one sitting at the min RGB corner and the other sitting in the max RGB corner. Those two cubes touch each other at just one corner point. Then, the two cubes are joined by an angled six sided pipe. Why so complex a shape. The real reason is not to have a complex shape. That is just the shape you get when using simple fast equations in software.
with their joined by a 6 sided pipe
Most of what one sees in PS is just 2D selections. An example of that is the prior posts by Tom Mann where he varied two colors in a gradient, one in X direction and the other in Y direction. If you take the selection boundary in the above picture and look at it end on to show only two of the dimensions of RGB values being selected you get a match with the selection shape demonstrated by Tom Mann:

In this next image, I leverage the test case Mr Tom suggested. I create a two dimensional gradient (41 pixel on a side) with green shifting in X and red shifting in Y. I copied this 41 sq pixel dual gradient 13 times and increased the rlue value from 0 (on left) by 2 for each 41 sq pixel. I sampled with the magic wand tool in at the cross hairs (contiguous was turned off) and the selected pattern in each 41 sq box is shown.
If you stack up the selections from the left to the right, you end up with the same 3D shape I shared above.

I have tested the above equations on a good number of examples and they all work. I don't mind trying out other suggested cases to see if they continue to fit.
Below are the 3D animated GIFS of the tolerance bounding box from the provided equations.

I followed through on this for my own satisfaction and may not have value for others yet thought it was still worth posting in case anyone wanted more clarity on the analysis or suggestions on what else to try and test the equations for correctness.





