Adjustment layer messes up when document is saved?

[Cheewii]

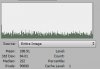
Hi guys this is kind of my first post requesting for help, I'm usually a lurker around here, but just this once I cannot for the life of me understand what's going on. Okay so I've basically edited an image I found, added another graphic and tweaked the atmosphere of the original photo and added some text. The last part is the stars, which I made by adding noise and then reducing the noise to faint stars using some adjustment layers.

Now I'm almost done now, and this is what I see in my final document:



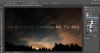
Looks perfectly fine right?

And now I try to save the PSD as a PNG file...and this happens:



Now something is definitely up with the Levels adjustment layer, but I have no idea what exactly and I can't solve it however I try. I've even tried merging most f the things together then applying a regular Levels adjustment from the "Image" tab but that doesn't work either.

Admittedly I'm not too familiar with adjustment layers even after learning Photoshop from the internet for two years but I've never had anything like this come up when I used them before.

Please help me with this bizarre problem! I've attached the PSD file below, you can open it and experiment with the layers in it to get a better sense of what's happening. (tell me if the attachments don't work)

View attachment An Airplane Carried Me To Bed 5.psd

Thanks!

 

[ibclare]

Try saving it as a jpeg instead of a png. Let me know how that works.

 

[Tom Mann]

First, I'll just point out to others that may be following along, your "Levels 1" layer is acting very much like a threshold adjustment layer acting on the noise layer immediately below, "Layer 5".

As an example of the real source of the problem, assume you change the viewing magnification from 100% down to 33.3%. When you do this, PS averages ~9 pixels (=3x3) to produce one pixel at the new magnification. This happens on every layer. Because the original noise pixels on Layer 5 are now averaged, these new pixels won't be distributed as widely in intensity as the original pixels -- more will be concentrated around mid-gray. Therefore, fewer will make it through your thresholding operation as one reduces the viewing magnification.

To verify this is indeed what is going on, simply view your image at a wide range of magnifications. You should see that at magnifications of 100% and any magnification above that, the number of "stars" that make it through your thresholding operation should hardly change. However, when you start to go significantly below 100% magnification, fewer stars should appear.

The fix is easy: bake in the number of stars that you want by generating a new "real" layer of stars (ie, not an adjustment layer) at 100%. Then, as you scale it up or down either in viewing magnification, or when turned into a jpg or a print of arbitrary size, the number of stars won't vary.

Pls. let me know how this works for you.

Cheers,

Tom

 

[Cheewii]

First, I'll just point out to others that may be following along, your "Levels 1" layer is acting very much like a threshold adjustment layer acting on the noise layer immediately below, "Layer 5".

As an example of the real source of the problem, assume you change the viewing magnification from 100% down to 33.3%. When you do this, PS averages ~9 pixels (=3x3) to produce one pixel at the new magnification. This happens on every layer. Because the original noise pixels on Layer 5 are now averaged, these new pixels won't be distributed as widely in intensity as the original pixels -- more will be concentrated around mid-gray. Therefore, fewer will make it through your thresholding operation as one reduces the viewing magnification.

To verify this is indeed what is going on, simply view your image at a wide range of magnifications. You should see that at magnifications of 100% and any magnification above that, the number of "stars" that make it through your thresholding operation should hardly change. However, when you start to go significantly below 100% magnification, fewer stars should appear.

The fix is easy: bake in the number of stars that you want by generating a new "real" layer of stars (ie, not an adjustment layer) at 100%. Then, as you scale it up or down either in viewing magnification, or when turned into a jpg or a print of arbitrary size, the number of stars won't vary.

Pls. let me know how this works for you.

Cheers,

Tom

Thank you very much! I could have never guessed this was the problem, it just never occurred to me that this could happen. I guess I do need a bigger screen after all Thank you for your help Tom, it helped me tremendously I have made a separate layer just for the stars and got a much better result, I owe this to you!

 

[Tom Mann]

I'm glad my explanation for this puzzling effect was useful.

I didn't mention in my last post that the fundamental reason for the change in shape of the histogram (ie, from flat and wide to a narrow peak) is something called the "Central Limit Theorem" of probability theory ( http://en.wikipedia.org/wiki/Central_limit_theorem ). I've illustrated it below. It shows one of the many wonderful connections between math and art, and especially math and Photoshop. Even better, anyone who owns a copy of PS can do this for themselves.

First, I show uniformly distributed random noise -- what it looks like, and its histogram:



I then took the noise (ie, first image above), and ran it through a Gaussian blur with a radius of 3 pixels, and show the resulting image and the histogram for it.



Note the dramatic change in the shape of the histogram, and also notice that the standard deviation (shown in Photoshop's info panel) has been reduced by a factor of around 10x!

The narrowing up of the histogram illustrates perfectly what the Central Limit Theorem predicts - averaging large numbers of identically distributed random numbers produces new random numbers (ie, new pixel values) whose histogram (in the limit of very large numbers of terms in the average, ie, large blur radii) approaches a Gaussian centered on the average of the original distribution. BTW, the reason that the average in my little example is not at 0.5 is because the calculations were done in a gamma weighted color space. If I had taken the time to switch over to a linear gamma space, the resulting peak would be exactly at 0.5.

We would love to see more of your work, so, if you like, please come back to the forum and chat, show off more of your very nice work, etc.

Best regards,

Tom M
Moderator, Photography Section
PSG